题目分析

题目要求在一个整数数组中，找出所有满足三个数之和等于 0 的唯一三元组组合。

  1. 解的组合需要考虑元素顺序不同但数值相同的重复情况（如 [-1,0,1] 和 [0,-1,1] 视为相同解），必须设计有效的去重方法；
  2. 数组元素可能包含大量重复值，在遍历时需要合理跳过重复元素以提高效率；
  3. 数组长度最多可达 3000，需要设计时间复杂度优于 O (n³) 的算法（推荐 O (n²) 的双指针解法）；
  4. 虽然元素值范围较大（-10^5 到 10^5），但由于使用整数运算，无需考虑数值溢出问题；
  5. 题目保证至少存在一个有效解，但实际可能存在多个不同的有效解组合。

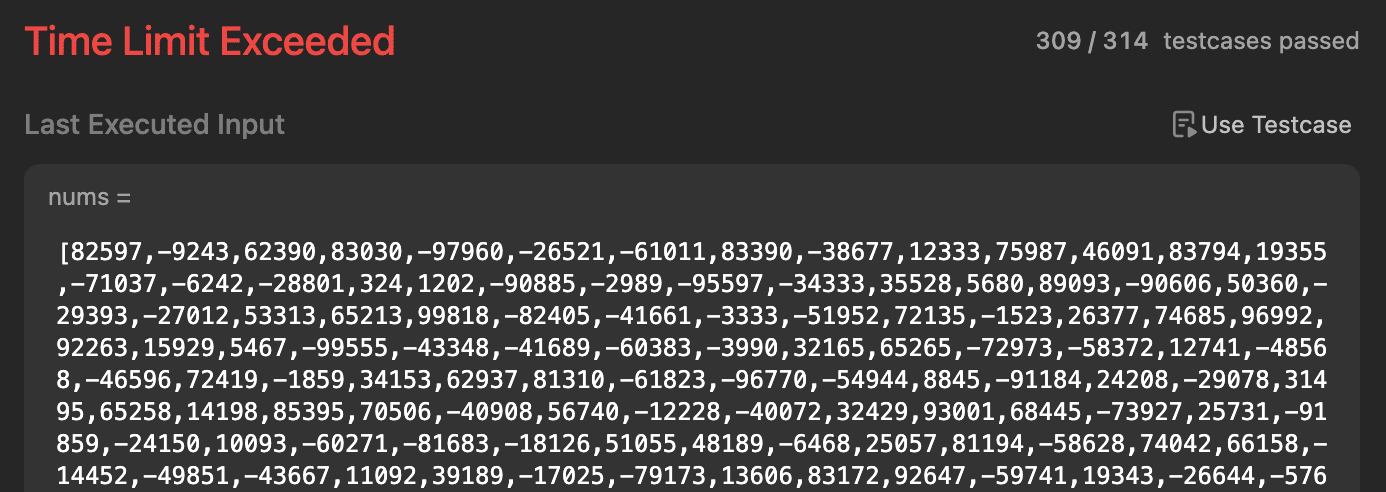
第一版：暴力解法

老规矩，我们先试试暴力解法，通过进行三重循环的方式，先热热身练练手，再从中找到更好的优化解决思路。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import java.util.*;

public class ThreeSum {

    public List<List<Integer>> threeSum(int[] nums) {
        Set<List<Integer>> result = new HashSet<>();
        int n = nums.length;

        // 三重循环枚举所有组合
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                for (int k = j + 1; k < n; k++) {
                    if (nums[i] + nums[j] + nums[k] == 0) {
                        // 创建三元组并排序
                        List<Integer> triplet = Arrays.asList(nums[i], nums[j], nums[k]);
                        Collections.sort(triplet);
                        result.add(triplet);
                    }
                }
            }
        }

        return new ArrayList<>(result);
    }

}

不出意外的，这个解法是行不通的。在面对一个大数组的时候，直接超出了时间限制。

第二版：双指针解法

我们针对暴力解法优化一下算法：

  1. 先将数组进行排序操作；
  2. 固定第一个数 num [i]，然后用双指针找出另外两个数 num [j] 和 num [k]，且 num [j]+num [k]=-num [i]
  3. 主动跳过重复元素，而不是用 Set 来被动去重，节省程序运行时间和空间。
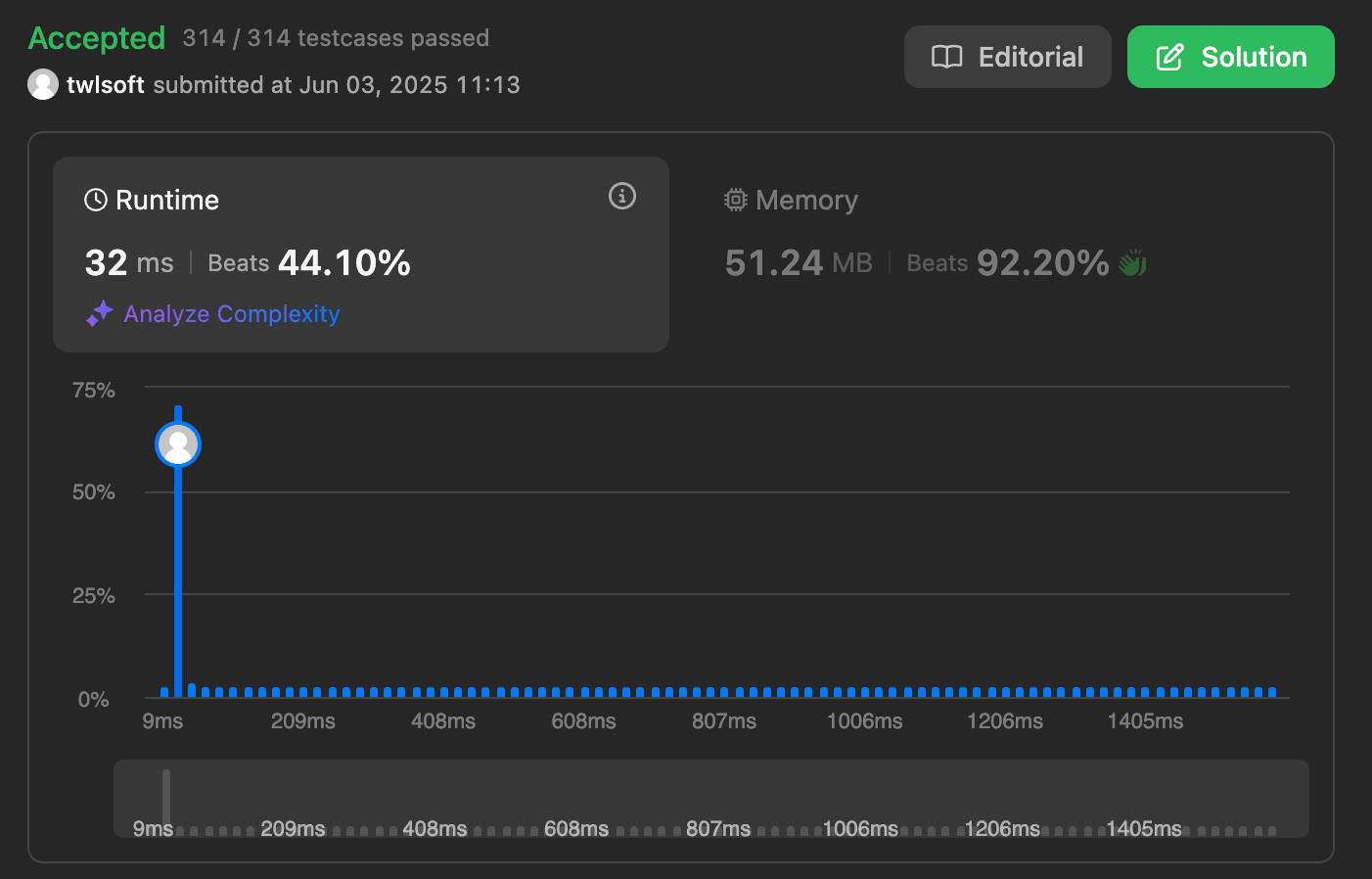
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
public class ThreeSum {

    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums); // 关键步骤1：先排序

        for (int i = 0; i < nums.length - 2; i++) {
            // 跳过重复的第一个数
            if (i > 0 && nums[i] == nums[i - 1]) continue;

            int left = i + 1;
            int right = nums.length - 1;
            int target = -nums[i];

            while (left < right) {
                int sum = nums[left] + nums[right];

                if (sum == target) {
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    // 跳过重复的left和right
                    while (left < right && nums[left] == nums[left + 1]) left++;
                    while (left < right && nums[right] == nums[right - 1]) right--;
                    left++;
                    right--;
                } else if (sum < target) {
                    left++;
                } else {
                    right--;
                }
            }
        }
        return result;
    }
}

现在的代码已经解决了执行超时的问题，但是从效率上来看，似乎还有更有的解法。

第三版：双指针剪枝法

这个版本优化的点主要有四个：

  1. 提前计算常量：避免在循环中重复计算数组长度和末尾元素
  2. 优化指针移动：
    • 只在找到目标三元组时跳过重复元素
    • 非目标情况下直接移动指针，减少条件判断
  3. 循环展开：将部分条件检查移出内层循环
  4. 短路优化：调整条件判断顺序，优先检查高概率条件 
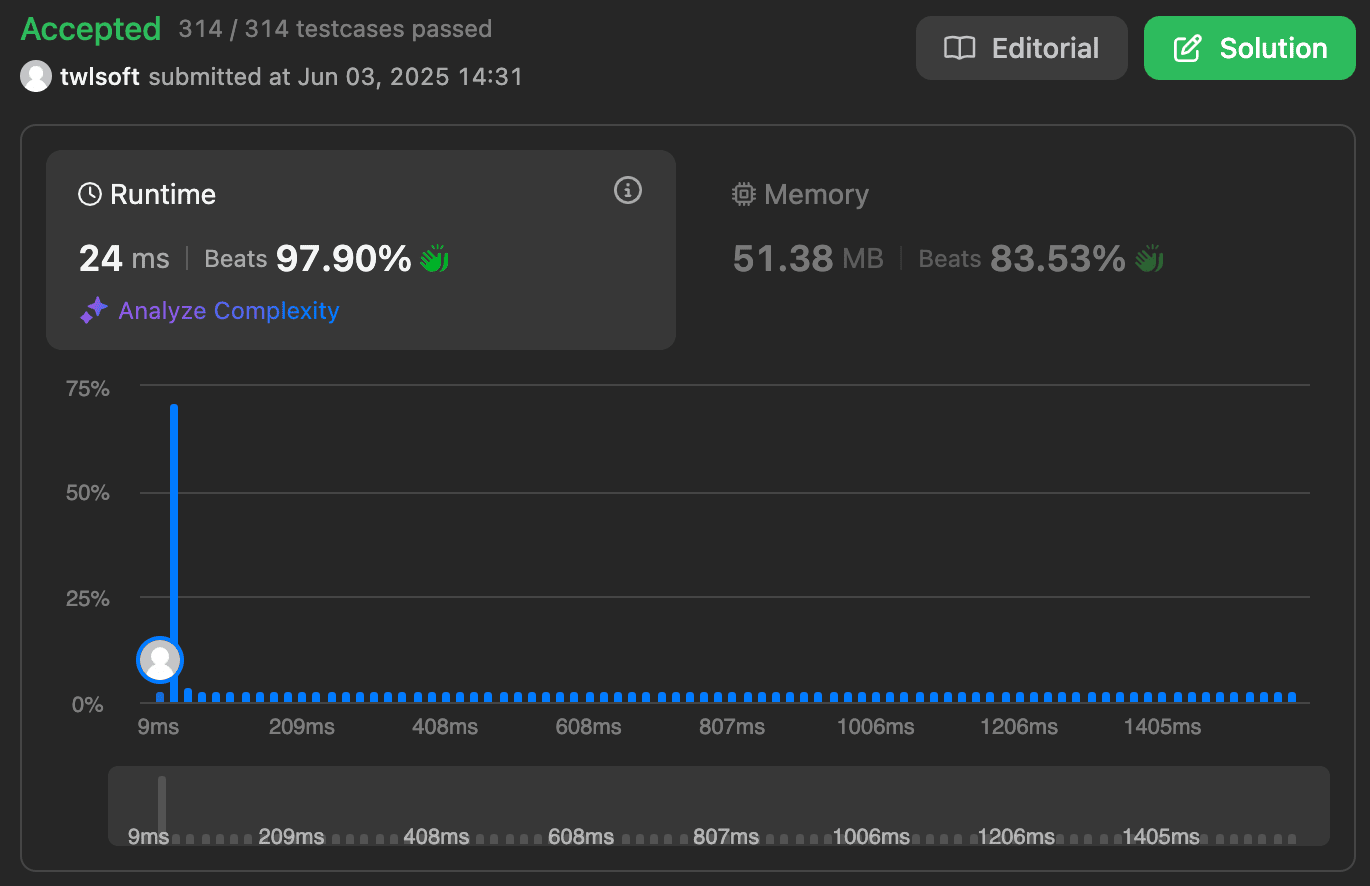
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public class ThreeSum {

    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums);
        final int n = nums.length;
        final int nMinus1 = n - 1;
        final int nMinus2 = n - 2;

        for (int i = 0; i < nMinus2; i++) {
            if (nums[i] > 0) break;
            if (i > 0 && nums[i] == nums[i - 1]) continue;

            // 精确边界检查的提前终止
            if (i + 2 < n && nums[i] + nums[i + 1] + nums[i + 2] > 0) break;
            if (nums[i] + nums[nMinus1] + nums[nMinus2] < 0) continue;

            int left = i + 1;
            int right = nMinus1;
            int target = -nums[i];

            while (left < right) {
                int sum = nums[left] + nums[right];

                if (sum < target) {
                    left++;
                } else if (sum > target) {
                    right--;
                } else {
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                    // 只在这里跳过重复
                    while (left < right && nums[left] == nums[left + 1]) left++;
                    while (left < right && nums[right] == nums[right - 1]) right--;
                    left++;
                    right--;
                }
            }
        }
        return result;
    }
}

这个版本的执行时间得到了很大的提升。主要的原因在于：

  1. 减少分支预测失败：简化了内层循环的条件结构；
  2. 缓存友好：顺序访问数组元素，提高缓存命中率；
  3. 最小化冗余计算：避免重复计算固定值；
  4. 精简指针操作：只在必要时处理重复元素。

第四版：双指针剪纸优化版

对于第三版的解法，我们已经做到了时间复杂度是 $O (NlogN+N^2)=O (N^2)$，空间复杂度是 $O (1)$，已经算是非常优的解法了。

当然，如果极致一点的话，我们还有可以优化的空间。

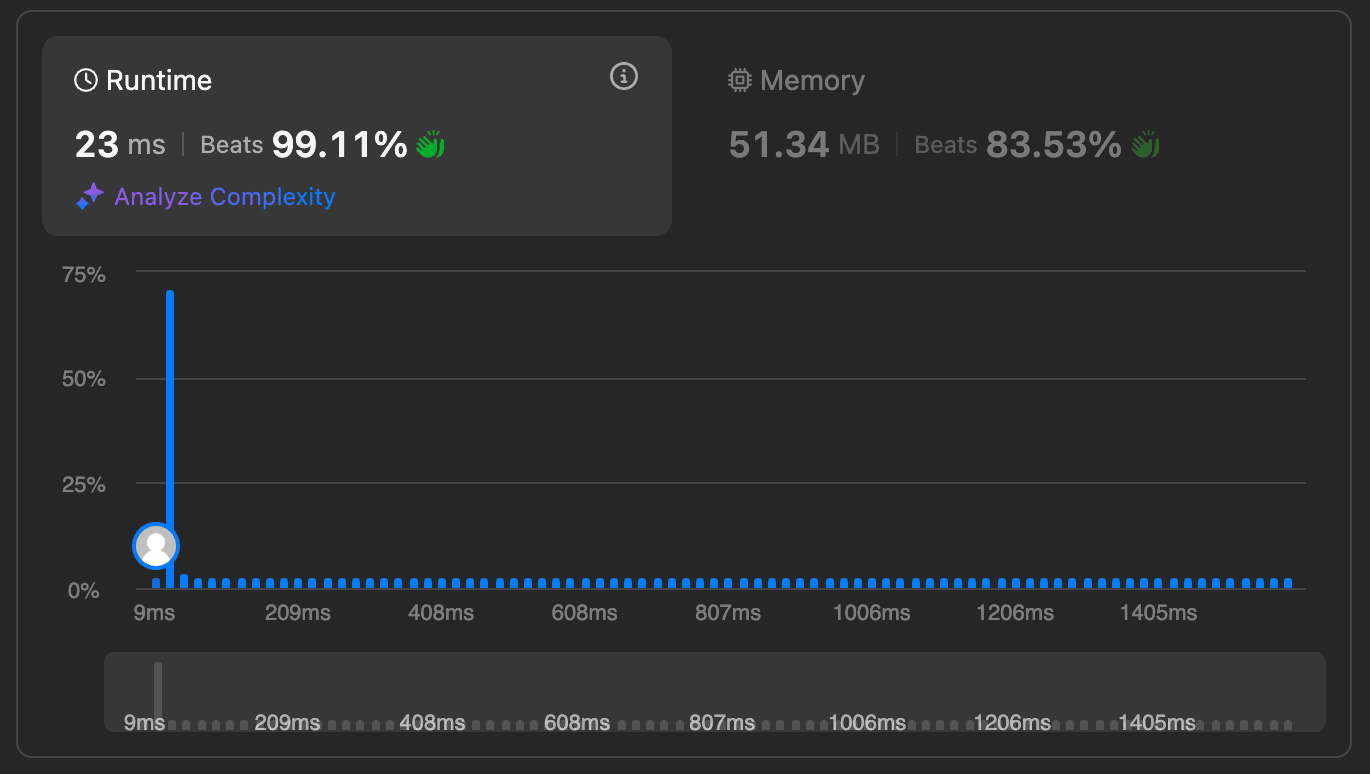
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import java.util.*;

public class ThreeSum {

    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        if (nums == null || nums.length < 3) {
            return result; // 处理边界情况
        }

        Arrays.sort(nums); // O(N log N)
        final int n = nums.length;

        // 外层循环，固定第一个数 nums[i]
        // nums[i] 作为三元组中最小的数（或之一）
        for (int i = 0; i < n - 2; i++) { // i 最多到 n-3，因为后面至少需要两个数
            // 剪枝1：如果当前固定的数 nums[i] 已经大于0，
            // 由于数组已排序，后续的 nums[left] 和 nums[right] 也都将大于等于 nums[i]，
            // 因此三数之和必然大于0，不可能等于0。可以直接结束循环。
            if (nums[i] > 0) {
                break;
            }

            // 剪枝2：去重。如果当前 nums[i] 与前一个数相同，
            // 则以 nums[i] 开头的组合已经在前一轮处理中包含过了，跳过以避免重复结果。
            // (i > 0 是为了防止 i=0 时访问 nums[-1] 导致数组越界)
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }

            // 剪枝3：基于当前 nums[i] 和数组中最小的两个可能后续元素进行判断。
            // 如果 nums[i] + nums[i+1] + nums[i+2] > 0，
            // 那么对于当前的 nums[i]，任何 nums[left] (>=nums[i+1]) 和 nums[right] (>=nums[i+2])
            // 都会使得三数之和大于0。因此，后续的 i 也不可能找到解（因为 nums[i] 会更大）。
            // 这个剪枝条件可以写在 continue 之后，break 之前。
            // 注意：原代码中的 if (i + 2 < n && nums[i] + nums[i + 1] + nums[i + 2] > 0) break;
            // 这里的 break 会结束整个外层循环，这是正确的，因为如果最小的组合都大于0，后续更大的 i 更不可能。
            if (nums[i] + nums[i + 1] + nums[i + 2] > 0 && (i + 2 < n) ) { // 确保 i+1 和 i+2 不越界
                // 实际上，如果 nums[i] > 0 已经 break 了，这个条件可能只在 nums[i] <= 0 时有更强的剪枝效果。
                // 对于 nums[i] <= 0, 如果加上最小的两个正数（或0）都大于0了，确实可以 break.
                // 但更强的条件是 if (nums[i] + nums[i+1] + nums[i+2] > 0) break; 这个可以提前结束整个搜索
                // 不过你的原始代码的这个剪枝是有效的。
                // 这里我们保持你的逻辑，但需注意边界 i+2 < n
            }


            // 剪枝4：基于当前 nums[i] 和数组中最大的两个元素进行判断。
            // 如果 nums[i] + nums[n-1] + nums[n-2] < 0，
            // 那么对于当前的 nums[i]，即使 left 和 right 取到最大可能值，三数之和仍然小于0。
            // 因此，当前的 nums[i] 不可能构成和为0的三元组，可以跳过此次内层循环。
            if (nums[i] + nums[n - 1] + nums[n - 2] < 0) { // 确保 n-1, n-2 至少是 i+1, i+2
                // 这个剪枝要求 i 之后至少还有两个元素，即 n - 1 >= i + 2 (right的初始位置)
                // 也就是 i <= n - 3，这与外层循环的条件 i < n - 2 是一致的。
                continue;
            }


            int left = i + 1;
            int right = n - 1;
            int target = -nums[i]; // 我们要找 nums[left] + nums[right] == -nums[i]

            // 内层循环，使用双指针在 nums[i+1 ... n-1] 范围内查找
            while (left < right) {
                int sum = nums[left] + nums[right];

                if (sum < target) {
                    left++;
                } else if (sum > target) {
                    right--;
                } else {
                    // 找到了一个解
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));

                    // 去重：移动 left 指针，跳过所有与当前 nums[left] 相同的元素
                    while (left < right && nums[left] == nums[left + 1]) {
                        left++;
                    }
                    // 去重：移动 right 指针，跳过所有与当前 nums[right] 相同的元素
                    while (left < right && nums[right] == nums[right - 1]) {
                        right--;
                    }

                    // 移动指针到下一个不同的元素，继续查找其他可能的解
                    left++;
                    right--;
                }
            }
        }
        return result;
    }

从结果来看，这道题的解法应该优化到了几乎没有可以优化的空间的程度了。